UJI KRUSKAL-WALLIS

click to get the pdf version

Kruskal-Wallis test dikembangkan oleh Kruskal dan Wallis. Uji Kruskal-Wallis adalah uji non-parametrik yang digunakan untuk membandingkan tiga atau lebih kelompok data sampel. Uji Kruskal-Wallis digunakan ketika asumsi ANOVA tidak terpenuhi. ANOVA adalah teknik analisis data statistik yang digunakan ketika kelompok-kelompok variabel bebas berjumlah lebih dari dua. Pada ANOVA, kita asumsikan bahwa distribusi dari masing-masing kelompok harus terdistribusi secara normal. Dalam uji Kruskal-Wallis, tidak diperlukan asumsi tersebut, sehingga uji Kruskal-Wallis adalah uji distribusi bebas. Jika asumsi normalitas terpenuhi, maka uji Kruskal-Wallis kita abaikan dan kita gunakan uji ANOVA. Penyusunan hipotesis dalam uji Kruskal Wallis adalah sebagai berikut:

H0 : sampel berasal dari populasi yang sama (µ1 = µ2 = … = µk)

H1 : sampel berasal dari populasi yang berbeda (µi = µj)

Uji Kruskal Wallis harus memenuhi asumsi berikut ini:

- Sampel ditarik dari populasi secara acak
- Kasus masing-masing kelompok independen
- Skala pengukuran yang digunakan biasanya ordinal
- Rumus umum yang digunakan pada uji kruskal wallis adalah :

Statistik uji Kruskal Wallis menggunakan nilai distribusi Chi-kuadrat dengan derajat bebas adalah k-1 dengan jumlah sample harus lebih dari 5. Jika nilai uji Kruskal Wallis lebih kecil daripada nilai chi-kuadrat tabel, maka hipotesis null diterima, berarti sampel berasal dari populasi yang sama, demikian pula sebaliknya.

Ilustrasi:

Berikut ini adalah hasil survey tingkat kepentingan terhadap 3 atribut yang dinotasikan dengan 1 adalah “terdapat banyak tenan-tenan terkenal”, 2 untuk “kelengkapan menu di foodcourt”, dan 3 untuk “frekuensi hiburan” pada sebuah Mall di kota X dimana pertanyaan terhadap ketiga atribut diambil secara acak. Jumlah responden sebanyak 30 orang dibagi ke dalam 3 kelompok. Setiap kelompok ditanyakan tingkat kepentingan terhadap masing-masing dari 3 atribut. Jawaban responden diidentifikasikan dengan skala likert, dimulai dari “1” untuk sangat penting, dan “5” untuk tidak penting.
Data yang diberikan adalah sebagai berikut:

Kali ini kita akan gunakan perangkat lunak IBM SPSS 23, kalau kamu menggunakan IBM SPSS 21 dan 22 langkahnya akan sama saja, plis cekidot below:

1. Input data seperti berikut (tahapannya ga akan dijelasi lagi disini, karena telah ada pada bahasan sebelumnya, silakan search aja di atas):

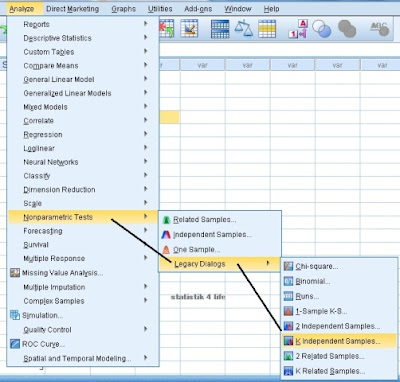
2. Kemudian pada menubar pilih Analyze – Non Parametric Test – Legacy dialogs - K-independent samples, seperti berikut:

3. Kemudian akan muncul kotak dialog, checklist kruskal wallis, kemudian masukkan variabel skor responden ke test variable list, dan atribut ke grouping variables, lalu klik define variable dan isikan dengan angka minimum atribut yaitu 1 dan maximum yaitu 3, klik continue seperti berikut:

Tampilannya jadi seperti ini, lihat grouping variables telah terinput atribut(1 3):

4. Kemudian pada jendela several independent samples, checklist beberapa indikator seperti pada gambar berikut, klik continue – OK

5. Kemudian hasilnya akan ditampilkan seperti berikut:

 

6. Interpretasi:

Nilai p-value sebesar 0,012 < nilai kritik 0,05, karena itu hipotesis null ditolak, bahwa terdapat cukup bukti dimana terdapat perbedaan dari ketiga kelompok responden dalam menilai tingkat kepercayaan terhadap ketiga atribut.(yoz)