click, to get pdf version
Korelasi merupakan hubungan antara dua buah variabel, jika nilai suatu variabel naik, sedangkan nilai variabel yang lain turun, maka dikatakan terdapat hubungan negatif serta sebaliknya. Korelasi yang biasa digunakan dalam penelitian adalah:
a. Korelasi Pearson Product Moment
Korelasi ini dilakukan jika sepasang variabel kontinu, memiliki korelasi. Jumlah pengamatan variabel X dan Y harus sama, atau kedua nilai variabel tersebut berpasangan. Semakin besar nilai koefisien korelasinya maka akan semakin besar pula derajat hubungan antara kedua variabel.
Korelasi Pearson biasanya pada hubungan yang berbentuk linier (keduanya meningkat atau keduanya menurun). Koefisien korelasi ini tidak menunjukkan adanya hubungan kausal antar variabelnya.
Contoh kasus: jika terdapat hubungan korelasi antara variabel citra merek dengan kepuasan konsumen motor merek Honda.
b. Korelasi Spearman
Jika pengamatan dari 2 variabel X dan Y adalah dalam bentuk skala ordinal, maka derajat korelasi dicari dengan koefisien korelasi spearman. Prosedurnya terdiri atas:
1. Atur Pengamatan dari kedua variabel dalam bentuk ranking.
2. Cari beda dari masing-masing pengamatan yang sudah berpasangan
3. Hitung koefisien korelasi Spearman dengan rumus:
ρ = 1 = 6∑d12 / N3 – N
dimana:
d1 = beda antara 2 pengamatan berpasangan
N = total pengamatan
ρ = koefisien korelasi spearman
Contoh aplikasi : jika seorang peneliti ingin melihat apakah ada korelasi antara kasus kematian pada ternak yang yang sakit dengan kematian ternak akibat stress, maka secara random diambil 10 sampel ternak.
Penyelesaian kasus tersebut secara manual dapat digunakan dengan langkah pemeringkatan terlebih dahulu pada kedua variabel (kematian karena sakit dan kematian karena stress).
c. Korelasi Rank Kendall
Analisis korelasi rank Kendall digunakan untuk mencari hubungan dan menguji hipotesis antara dua variabel atau lebih, bila datanya berbentuk ordinal atau ranking. Kelebihan metode ini bila digunakan untuk menganalisis sampel berukuran lebih dari 10 dan dapat dikembangkan untuk mencari koefisien korelasi parsial.
Metode yang digunakan pada analisis koefisien korelasi rank Kendall yang diberi notasi τ adalah sebagai berikut.
1. Beri ranking data observasi pada variabel X dan variabel Y.
2. Susun n objek sehingga ranking X untuk subjek itu dalam urutan wajar, yaitu 1, 2, 3, …, n. Apabila terdapat ranking yang sama maka ranking-nya adalah rata-ratanya.
3. Amati ranking Y dalam urutan yang bersesuaian dengan ranking X yang ada dalam urutan wajar kemudian tentukan jumlah angka pasangan concordant (Nc) dan jumlah angka pasangan discordant (Nd).
4. Statistik uji yang digunakan:
τ = Nc – Nd / (N(N-1)/2)
dimana:
τ = koefisien korelasi rank Kendall
Nc = jumlah angka pasangan concordant
Nd = jumlah angka pasangan discordant
N = ukuran sampel
Aplikasi korelasi Rank Spearman, Pearson dan Rank Kendall menggunakan software SPSS.17.0 adalah sebagai berikut:
Jika kita memiliki data produksi dan data ekspor suatu komoditi, kita ingin melihat hubungan antara keduanya (apakah ada korelasi antara total produksi dan ekspor).
1. Buka program SPSS kemudian input data ke dalam tabel-tabel SPSS:
2. Klik dari menubar Analyze – Correlate – Bivariate, seperti berikut:
3. Kemudian masukkan kedua variabel ke kotak variables di sebelah kanan, checklist koefisien korelasi sebagai “Pearson” atau “Rank Kendall” atau “Spearman”, dalam contoh ini kita menggunakan korelasi pearson product moment, gambar berikut:
4. Kemudian Klik OK
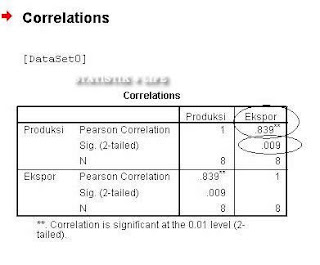
Maka akan muncul output sebagai berikut:
Dari output di atas, N menunjukkan jumlah observasi/sampel sebanyak 8, sedangkan hubungan korelasi ditunjukkan oleh angka 0,839(**) yang artinya besar korelasi yang terjadi antara variabel X dan Y adalah baik yaitu sebesar 0,839.
Sedangkan angka sig.(2-tailed) adalah 0,009 masih lebih kecil daripada batas kritis α = 0,05 (0,009 < 0,05), berarti terdapat hubungan yang signifikan antara kedua variabel.
Cara yang sama dengan menggunakan SPSS dapat dilakukan juga terhadap korelasi Rank Kendall maupun Spearman.
Sumber: Nazir, M. 2003. Metode Penelitian. Ghalia Indonesia: Jakarta